Šta je optimizacija?
Optimizacija je grana matematike koja se bavi proučavanjem i rešavanjem problema u kojima se traži rešenje koje je „najbolje“ pri određenim uslovima. Nalaženje optimalnog rešenja je nešto sa čime se srećemo u svakodnevnom životu i što nas okružuje. Svako od nas traži najkraću putanju od kuće do posla i raduje se svakoj novoj pronađenoj prečici (boljem rešenju) koja smanjuje vreme putovanja. Cilj svakog preduzetnika je povećanje profita, što se može posmatrati kao problem minimizacije njegovih troškova ili maksimizacije efikasnosti proizvodnje. Investitorima je bitno da što više smanje rizik investicionog portfolija, a da prinos bude što veći. Ali ne samo to, nije čovek jedini koji teži optimalnosti. Fizički sistemi teže stanju sa minimalnom energijom, molekuli u izolovanom hemijskom sistemu interaguju sve dok se potencijalna energija njihovih elektrona ne svede na minimum. Na osnovu priloženog, možemo stvoriti sliku o tome koliko je važno naći optimalno rešenje i posvetiti se razvoju aparata koji nam to omogućava.

U zavisnosti od kriterijuma podele, postoje razne podoblasti optimizacije. Ukoliko nemamo tzv. ograničenja u matematičkom modelu, onda govorimo o bezuslovnoj optimizaciji, inače je u pitanju uslovna optimizacija. Ukoliko potencijalno rešenje problema pripada nekom konačnom (ali često ogromnom) skupu, onda govorimo o diskretnoj optimizaciji, u suprotnom reč je o kontinualnoj optimizaciji. Kontinualnoj optimizaciji pripadaju varijacioni račun, optimalno upravljanje, teorija ekstremalnih problema i slične discipline. U zavisnosti od toga da li tražimo lokalno najbolje rešenje ili tražimo najbolje među svim rešenjima iz dopustivog skupa, razlikujemo lokalnu i globalnu optimizaciju.
Problemi diskretne optimizacije nalaze veliku primenu u najrazličitijim oblastima teorije (logici, teoriji grafova) i prakse gde je zadatak rešiti neki realan problem: optimalno upravljanje proizvodnjom, problem pakovanja, raspoređivanja poslova na mašinama, transport gotovih proizvoda, nalaženje optimalnih lokacija za izgradnju postrojenja, uslužnih ili distributivnih centara, optimalno planiranje telekomunikacione mreže itd.
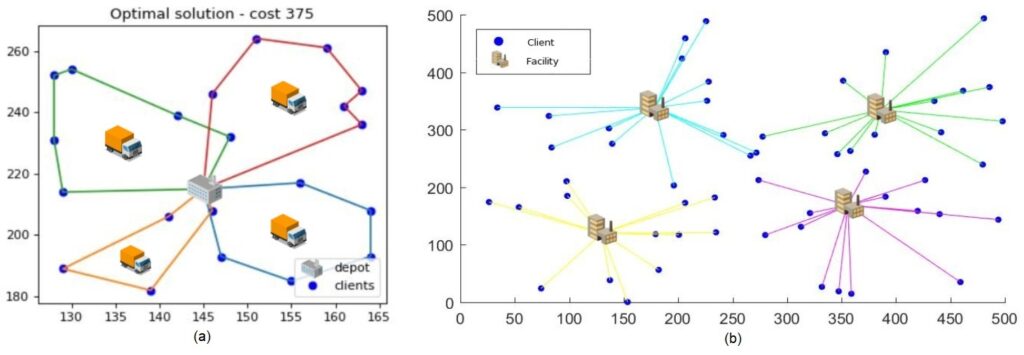
Nakon što formiramo matematički model, možemo iskoristiti neki postojeći metod (algoritam) koji nalazi rešenje zadatka, obično uz pomoć računara. Ne postoji univerzalni algoritam koji rešava svaki optimizacioni problem, već imamo skup algoritama od kojih biramo (ili sami formiramo) onaj koji je „prilagođen“ našem problemu. Na osnovu tipa problema biramo grupu metoda, a potom i sam algoritam koji ćemo koristiti kako bismo u što kraćem vremenu izvršavanja došli do što kvalitetnijeg rešenja. Metode za rešavanje optimizacionih problema se pre svega dele na egzaktne (nalaze tačno rešenje problema) i aproksimativne metode (aproksimiraju rešenje sa određenom tačnošću). Osnovna mana egzaktnih metoda je njihovo vreme izvršavanja, koje često zna biti nedopustivo dugo, što ih čini neupotrebljivim. Sa druge strane, aproksimativne metode nalaze kvalitetna rešenja u dosta kraćem vremenu izvršavanja.
U poslednje vreme intenzivno se razvijaju metaheuristički algoritmi, jedna vrsta aproksimativnih algoritama koji uspevaju da u realnom vremenu pronađu kvalitetna rešenja (neretko i optimalna). Zasnovane su na skupu uopštenih pravila na visokom apstraktnom nivou što omogućava široku primenu u rešavanju najrazličitijih problema optimizacije. Da bi heuristika vodila ka visoko kvalitetnim rešenjima, njeni elementi i koraci moraju u velikoj meri biti zasnovani na specifičnostima konkretnog problema koji se rešava. Posebnu pažnju privlače metaheuristike koje su inspirisane biološkom evolucijom i oponašanjem prirodnih i društvenih procesa.
Varijacioni račun i optimalno upravljanje
Neki od osnovnih problema optimizacije u funkcionalnim prostorima su problemi varijacionog računa i optimalnog upravljanja.
Varijacioni račun је relativno stara matematička disciplina. Može se reći da je varijacioni račun „rođen“ 1697. godine u Groningenu kada je Johan Bernuli publikovao svoje rešenje tzv. brahistohronog problema. Teorijske osnove klasičnog varijacionog računa postavili su Ojler i Lagranž u 18. veku. Tokom 18. i 19. veka njim su se bavili mnogi veliki matematičari: Ležandr, Jakobi, Hamilton, Vaještras i Hilbert. Ovaj poslednji mu је posvetio i jedan od svojih značajnih problema. Za više informacija videti Hilbertove probleme.
Osnovni zadatak varijacionog računa je nalaženje funkcije za koju dati integralni funkcional postiže ekstremnu vrednost. Te funkcije su najčešće glatke i prolaze kroz date granične tačke.

Optimalno upravljanje је znatno mlađe оd varijacionog računa. Nastalo је pedesetih godina prošlog veka. Klasičini varijacioni račun nije mogao da reši mnoge inženjerske probleme savremenog doba, pre svega оnе vezane za kosmičke letove. То је iniciralo nastanak nove matematičke discipline. Obično se za godinu nastanka optimalnog upravljanja uzima 1956. kada је kao hipoteza formulisan Pontrjaginov princip maksimuma.
Poznato je da se dinamički proces odvija u nekom sistemu čije se stanje u svakom vremenskom trenutku opisuje nekom funkcijom stanja. Osnovni zadatak optimalnog upravljanja je ispunjavanje određenog kriterijuma optimalnosti za dati sistem. Problemi varijacionog računa i optimalnog upravljanja nalaze veliku primenu u najrazličitijim oblastima fizike, mašinstva, ekonomije, avioindustrije, aeronautike, brodogradnje, automobilske i vojne industrije gde je zadatak rešiti neki realan problem. Recimo, to su optimalno vreme putovanja svetlosti, problemi optimalne putanje broda i aviona, maksimizacija profita određene kompanije, optimalno sletanje letelica na planete ili satelite u svemiru što podrazumeva sletanje za najkraće vreme.
Studenti će na ovom Modulu iz oblasti optimizacije savladati rad u nekoliko programskih jezika i softvera (C, Java, MatLab, Lingo, Cplex…) kroz koje će, osim njihove sintakse, naučiti i različite metode (egzaktne i aproksimativne) za rešavanje najčešćih optimizacionih problema iz realnog života i kako se oni implementiraju na računarima.
