Šta je numerička matematika?
Numerička matematika je matematička disciplina koja stupa na snagu onda kada klasična matematička analiza nema odgovore na neka određena pitanja. Dok je u klasičnoj analizi cilj odrediti rešenje nekog zadatka, opisati njegove osobine i odrediti pod kojim uslovima to rešenje postoji, numerička matematika efikasno nalazi to rešenje sa nekom dozvoljenom greškom. Numeričke metode se razvijaju kako bi se rešio neki matematički model koji najčešće opisuje neki proces ili pojavu iz sveta koji nas okružuje.
Nekada, osim numeričkog, drugo rešenje i ne možemo naći ili nam nije ni potrebno. Poznato je da se integrali za neke funkcije, koje su od značaja u matematičkoj statistici, ne mogu zapisati pomoću elementarnih funkcija. Pa ipak, određeni integrali tih funkcija su jedinstvene vrednosti do kojih se može doći samo numeričkim metodama. One nas najčešće neće dovesti do tačnog rešenja, ali suština je u tome što možemo dobiti rešenje sa kolikom god željenom tačnošću. Zato je verni pratilac svake numeričke metode analiza greške, kako same metode, tako i tzv. greške računa.


Napredne numeričke metode su esencijalne u meteorološkim predviđanjima. Automobilske kompanije mogu da povećaju bezbednost vozila koristeći simulacije automobilskih udesa koje se zasnivaju na numeričkom rešavanju parcijalnih diferencijalnih jednačina. Proračunavanje putanje nebeskih tela ili letelica i satelita zasnivaju se na numeričkim metodama za rešavanje sistema običnih diferencijalnih jednačina, čime je numerička matematika postala deo nebeske mehanike. Obrada strujnih, zvučnih, govornih i video signala, filtriranje šumova, prepoznavanje oblika i drugo, samo su još neki od primera moderne primene ove grane matematike.
Osnovni zadatak numeričke matematike je razvoj (numeričkih) metoda kojima se vrši prilagođavanje apstraktnih matematičkih modela mogućnostima računarske tehnike. Kako se na računarima izvršavaju samo osnovne računske operacije, jedan od prvih problema numeričke matematike je kako u takvom sistemu predstaviti elementarne funkcije kao što su cos(x) ili ex. Kako aproksimirati proizvoljnu funkciju?

Problemom aproksimacije funkcija se bavi polje numeričke matematike, koje se naziva Teorija aproksimacija. Može se reći da je njen razvoj započeo još u 18. veku. Matematičari koji su dali najveći doprinos na tom polju bili su Lagranž, Čebišev, Jakobi, Vaještras, Runge, Lebeg, Poason i drugi. Ovom problematikom naučnici se aktivno bave i danas.
Kako je razvoj računarstva stalno u ekspanziji, time su i mogućnosti za realizaciju složenijih matematičkih modela sve veće i veće. Takvi modeli često sadrže diferencijalne i/ili parcijalne diferencijalne jednačine, pa se razvoju numeričkih metoda za ovakve probleme posvećuje posebna pažnja. Izučavanje numeričkih metoda uključuje i analizu greške, stabilnosti i konvergencije metoda. Zbog toga se ovaj deo numeričke matematike naziva numerička analiza. Ona se oslanja na više matematičkih disciplina, od kojih u poslednje vreme vidno mesto zauzima funkcionalna analiza.
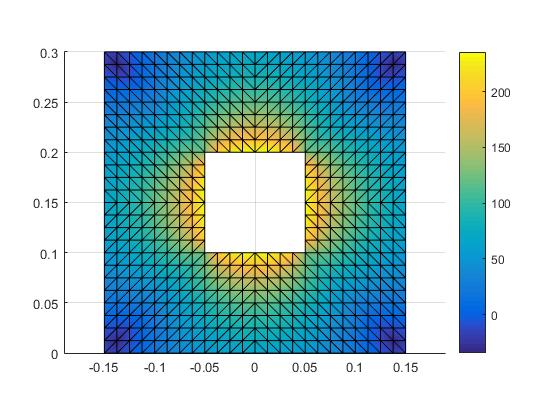
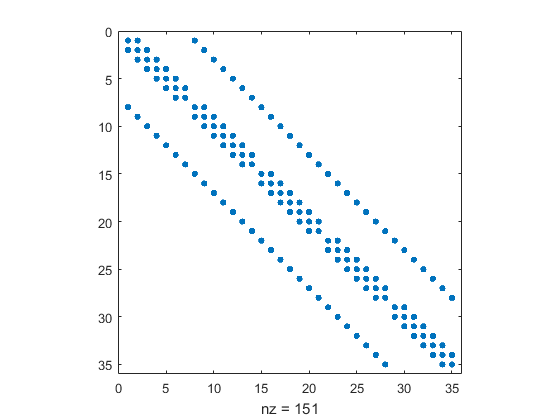
Numeričke metode za rešavanje linearnih diferencijalnih i parcijalnih diferencijalnih jednačina često se svode na sisteme linearnih jednačina. U praksi se radi sa sistemima od više hiljada nepoznatih, gde klasični aparat linearne algebre postaje neupotrebljiv. Stoga je razvoj stabilnih (računska greška se ne akumulira) i efikasnih (što manji broj računskih operacija) numeričkih algoritama veoma važan, čime se bavi numerička linearna algebra. Neretko ti sistemi imaju specifičnu strukturu u obliku retke matrice, tj. matrice koja ima veliki broj nula, pa se i numeričke metode prilagođavaju kako bi iskoristile tu osobinu.
Studenti će na ovom Modulu naučiti uvodne elemente iz teorije numeričke matematike i da rade sa približnim brojevima i funkcijama. Naučiće najbolje vrste aproksimacija funkcija, numeričko diferenciranje i integraciju, kao i numeričko rešavanje osnovnih zadataka linearne algebre u koje spadaju rešavanje sitema linearnih jednačina, nalaženje inverza matrice i njene determinante kao i određivanje sopstvenih vrednosti. Takođe će izučiti numeričke metode za rešavanje nelinearnih jednačina i sistema istih. Sledeći nivo nadogradnje znanja je iz oblasti običnih i parcijalnih diferencijalnih jednačina. Studenti imaju priliku da nauče o metodama za numeričko rešavanje takvih jednačina u okviru tzv. numeričke analize.
Gotovo sve numeričke metode koje studenti izuče, imaće priliku da implementiraju na računarima. Studenti će se upoznati sa programskim jezicima C i Java, a numeričke metode će implementirati u programskom paketu MatLab, savremenom okruženju za numerička izračunavanja. Osim toga imaće priliku da se upoznaju sa programskim jezicima Fortran, C++ i Phyton.
