What is optimization?
Optimization is a branch of mathematics that deals with the study and solution of problems in which the "best" solution under certain conditions is sought. The search for the optimal solution is something we encounter and are surrounded by in our daily lives. Each of us is in search of the shortest way from home to work and is happy about every new shortcut (better solution) that shortens the travel time. The goal of every entrepreneur is to increase profit, which can be seen as a problem of minimizing costs or maximizing production efficiency. For investors, it is important to reduce the risk of the investment portfolio as much as possible and make the return as high as possible. But it is not only humans that strive for optimality. Physical systems strive for a state with minimal energy; molecules in an isolated chemical system interact until the potential energy of their electrons is reduced to a minimum. From the attached, we can get an idea of the importance of finding an optimal solution and dedicate ourselves to developing devices that allow us to do so.

Depending on the partition criteria, there are different parts of the optimization. If there are no so-called constraints in the mathematical model, it is an unconstrained optimization, otherwise it is a constrained optimization. If the potential solution of the problem belongs to a finite (but often huge) set, then it is called discrete optimization, otherwise it is called continuous optimization. Calculus of variations, optimal control, theory of extreme problems and similar disciplines belong to continuous optimization. Depending on whether we are looking for the local best solution or the best of all solutions from the admissible set, we distinguish between local and global optimization.
Discrete optimization problems are widely used in various fields of theory (logic, graph theory) and practice when solving a real-world problem: optimal production management, the problem of packaging, scheduling orders on machines, transporting finished products, finding optimal locations for building factories, service or distribution centers, optimal planning of the telecommunications network, etc.
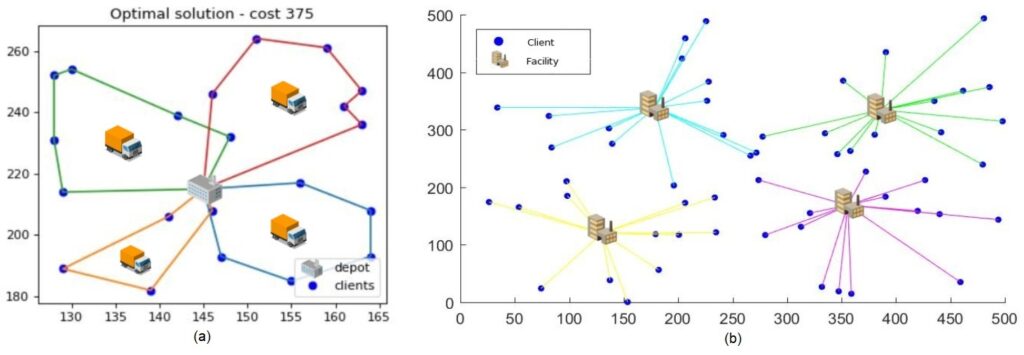
After creating a mathematical model, we can use an existing method (algorithm) that finds a solution to the problem, usually with the help of a computer. There is no universal algorithm that solves every optimization problem, but there are a number of algorithms from which we choose (or develop ourselves) the one that is "adapted" to our problem. Based on the nature of the problem, we select a group of methods and then the algorithm itself that we use to arrive at a high-quality solution in the shortest execution time. Methods for solving optimization problems are primarily divided into exact (exact solution of the problem) and approximate methods (approximating the solution with a certain accuracy). The main drawback of exact methods is their execution time, which can often be unacceptably long, making them unusable. Approximate methods, on the other hand, find high-quality solutions in much shorter execution time.
Recently, metaheuristic algorithms have been intensively developed, a type of approximation algorithm capable of finding high-quality (often optimal) solutions in real time. They are based on a set of general rules at a high level of abstraction, which allows for wide application in solving a variety of optimization problems. For heuristics to lead to high-quality solutions, their elements and steps must be based largely on the specifics of the problem being solved. Metaheuristics inspired by biological evolution and the imitation of natural and social processes receive special attention.
The calculus of variations and optimal control
Some of the basic optimization problems in functional spaces are the calculus of variations and optimal control.
The calculus of variations is a relatively old mathematical discipline. It can be said that the calculus of variations was "born" in Groningen in 1697, when Johann Bernoulli published his so-called solution of the brachistochronic problem. The theoretical foundations of the classical calculus of variations were laid in the 18th century by Euler and Lagrange. During the 18th and 19th centuries, many great mathematicians dealt with it: Legendre, Jacobi, Hamilton, Vajestras and Hilbert. The latter also dedicated one of his important problems to it. For more information, see Hilbert's problems.
The basic task of calculus of variations is to find a function for which a given integral functional reaches an extreme value. These functions are usually smooth and pass through certain boundary points.

Optimal control is much younger than the calculus of variations. It was developed in the fifties of the last century. The classical calculus of variations could not solve many technical problems of modern times, especially those related to space travel. This initiated the emergence of a new mathematical discipline. Usually, 1956 is considered the year of the emergence of optimal control, when Pontryagin's maximum principle was formulated as a hypothesis.
It is well known that a dynamic process takes place in a system whose state at each instant is described by a state function. The basic task of optimal control is to satisfy a certain optimality criterion for a given system. The problems of calculus of variations and optimal control are used in various fields of physics, mechanical engineering, economics, aeronautics, space, shipbuilding, automotive and military industries, where the objective is to solve a real-world problem. It is, for example, the optimal travel time of light, the problem of the optimal route of ships and airplanes, maximizing the profit of a particular company, the optimal landing of aircraft on planets or satellites in space, that is, landing in the shortest time.
In this optimization module, students master the work in different programming languages and software (C, Java, MatLab, Lingo, Cplex...), through which they learn not only their syntax but also different methods (exact and approximate) for solving the most common optimization problems from real life and their implementation on the computer.
